Privacy and Fairness in Model Partitioning
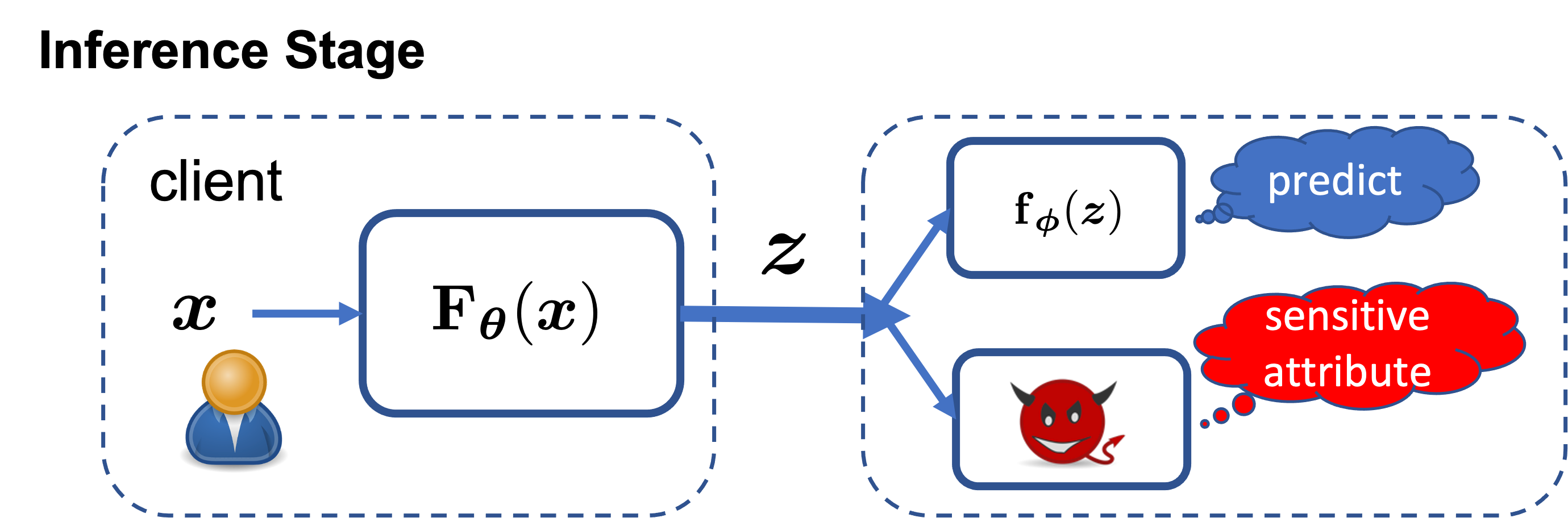
Deep learning sits at the forefront of many on-going advances in a variety of learning tasks. Despite its supremacy in accuracy under benign environments, Deep learning suffers from adversarial vulnerability and privacy leakage in adversarial environments. To mitigate privacy concerns in deep learning, the community has developed several distributed machine learning schemes, such as model partitioning. Model partitioning divides the deep learning model into a client partition and a server partition. As shown in the figure below, instead of sharing data $\mathbf{\mathit{x}}$ with the server, the users feed their data into the client partition $\mathbf{F}_{\mathbf{\mathit{\theta}}}(\cdot)$ and send the output representations $\mathbf{\mathit{z}}$ to the server. The server can feed the representations into the server partition $\mathbf{f}_{\mathbf{\mathit{\phi}}}(\cdot)$ to make predictions.
Although model partitioning addresses the direct privacy leakage from the raw data, it cannot prevent indirect privacy leakage from the representations since the representations may memorize sensitive information from the data. In particular, recent work shows that the potential adversary, with the access to the representations, can infer the associated sensitive attributes such as gender and race. Beyond privacy concerns, deep learning also suffers from substantial group fairness issues. Due to data inadequacy or bias, many machine learning and deep learning models exhibit discriminatory behaviors against certain groups of subjects. In this regard, the community has proposed the concept of demographic (statistical) parity to mathematically define group fairness and several approaches to mitigating demographic (statistical) disparity in machine learning and deep learning. But the effectiveness of those mitigation approaches are limited.
An Information-Theoretic Framework
To alleviate the privacy and fairness concerns, we propose a unified information-theoretic framework to defend against sensitive attribute inference and mitigate demographic disparity for the model partitioning scenario, by minimizing two mutual information terms. In particular, we prove information-theoretic bounds on the chance for any adversary to infer the sensitive attribute from model representations and the extent of demographic disparity, as introduced below.
Sensitive Attribute Inference. For a general sensitive attribute $\mathbf{\mathit{s}}$ such as gender and race, the chance for any adversary to infer $\mathbf{\mathit{s}}$ from the representation $\mathbf{\mathit{z}}$ can be bounded by $$\mathbb{P}[\hat{\mathbf{\mathit{s}}} = \mathbf{\mathit{s}}] \leq \frac{I(\mathbf{\mathit{z}}; \mathbf{\mathit{s}}) + \log 2}{\log |\mathcal{S}|},$$ where $\hat{\mathbf{\mathit{s}}}$ is the attribute inferred by the adversary, and $\mathbb{P}[\hat{\mathbf{\mathit{s}}} = \mathbf{\mathit{s}}]$ is the inference chance. $I(\mathbf{\mathit{z}}; \mathbf{\mathit{s}})$ refers to the mutual information between the representation $\mathbf{\mathit{z}}$ and the attribute $\mathbf{\mathit{s}}$.
Demographic Disparity. The definition of demographic parity is that the model prediction distribution conditional on the attribute $p(\hat{\mathbf{\mathit{y}}}|\mathbf{\mathit{s}})$ is equal to the unconditional model prediction distribution $p(\hat{\mathbf{\mathit{y}}})$, which means the predictions distribute fairly across groups with different attribute values such as different genders and races. Based on the definition of demographic parity, we naturally define the extent of demographic disparity as the difference between $p(\hat{\mathbf{\mathit{y}}}|\mathbf{\mathit{s}})$ and $p(\hat{\mathbf{\mathit{y}}})$, then the extent of demographic disparity can be bounded by
$$\sum_{\hat{\mathbf{\mathit{y}}}\in\mathcal{Y}}|p(\hat{\mathbf{\mathit{y}}}|\mathbf{\mathit{s}}) - p(\hat{\mathbf{\mathit{y}}})|\leq \sqrt{2|\mathcal{S}|\cdot I(\hat{\mathbf{\mathit{y}}}; \mathbf{\mathit{s}})},$$
where $I(\hat{\mathbf{\mathit{y}}}; \mathbf{\mathit{s}})$ refers to the mutual information between the prediction $\hat{\mathbf{\mathit{y}}}$ and the attribute $\mathbf{\mathit{s}}$.
Given the above theoretical results, we propose to minimize $I(\mathbf{\mathit{z}}; \mathbf{\mathit{s}})$ and $I(\hat{\mathbf{\mathit{y}}}; \mathbf{\mathit{s}})$ to mitigate sensitive attribute inference and demographic disparity. Since direct optimization on the mutual information is intractable, we further propose a tractable Gaussian mixture based method and a gumbel-softmax trick based method for estimating the two mutual information terms. Extensive evaluations in a variety of application domains, including computer vision and natural language processing, demonstrate our framework’s overall better performance than the existing baselines. Authored by Tianhang Zheng, this work has been published in the Proceedings of AsiaCCS 2022.