Distributed Inference of Deep Learning Models
Deep learning models are typically deployed at remote cloud servers and require users to upload local data for inference, incurring considerable overhead with respect to the time needed for transferring large volumes of data over the Internet. An intuitive solution to reduce such overhead is to offload these inference tasks from the cloud server to the edge devices. Unfortunately, edge devices are typically resource-constrained while the inference process is extremely computation-intensive. Directly using a deep learning model for inference on devices with limited computation power may result in an even longer inference time. For this reason, it is desirable to design distributed inference mechanisms that accelerate the inference process by partitioning the workload and distributing them to a cluster of edge devices for cooperative inference.
However, existing works generally assume that deep learning models are constructed as a chain of sequentially executed layers. Unfortunately, such an assumption is too simplified to hold with modern deep learning models: besides stacking deeper layers, structural modifications are also applied to the models to pursue the best performance. Generally, modern models are constructed as directed acyclic graphs (DAGs), rather than chains to represent complicated layer dependencies. For example, a layer may require outputs from multiple preceding layers, or its output has to be fed into multiple subsequent layers.
In this work, we propose EdgeFlow, a new distributed inference mechanism specifically designed for general DAG structured deep learning models. To maintain the layer dependencies in the original model, EdgeFlow breaks layers of the computation graph into a set of execution units, which contain a list of input requirements, the computation operator, and a forwarding table. During the inference, when the required input is ready, the execution unit will apply the computation operator on the input to get an intermediate result. According to the forwarding table, it will send the intermediate result to other units to fulfill their input requirements. Intuitively, the intermediate results flow among execution units that are distributed among edge devices according to the dependency to finish a logically equivalent inference as the original computation graph.
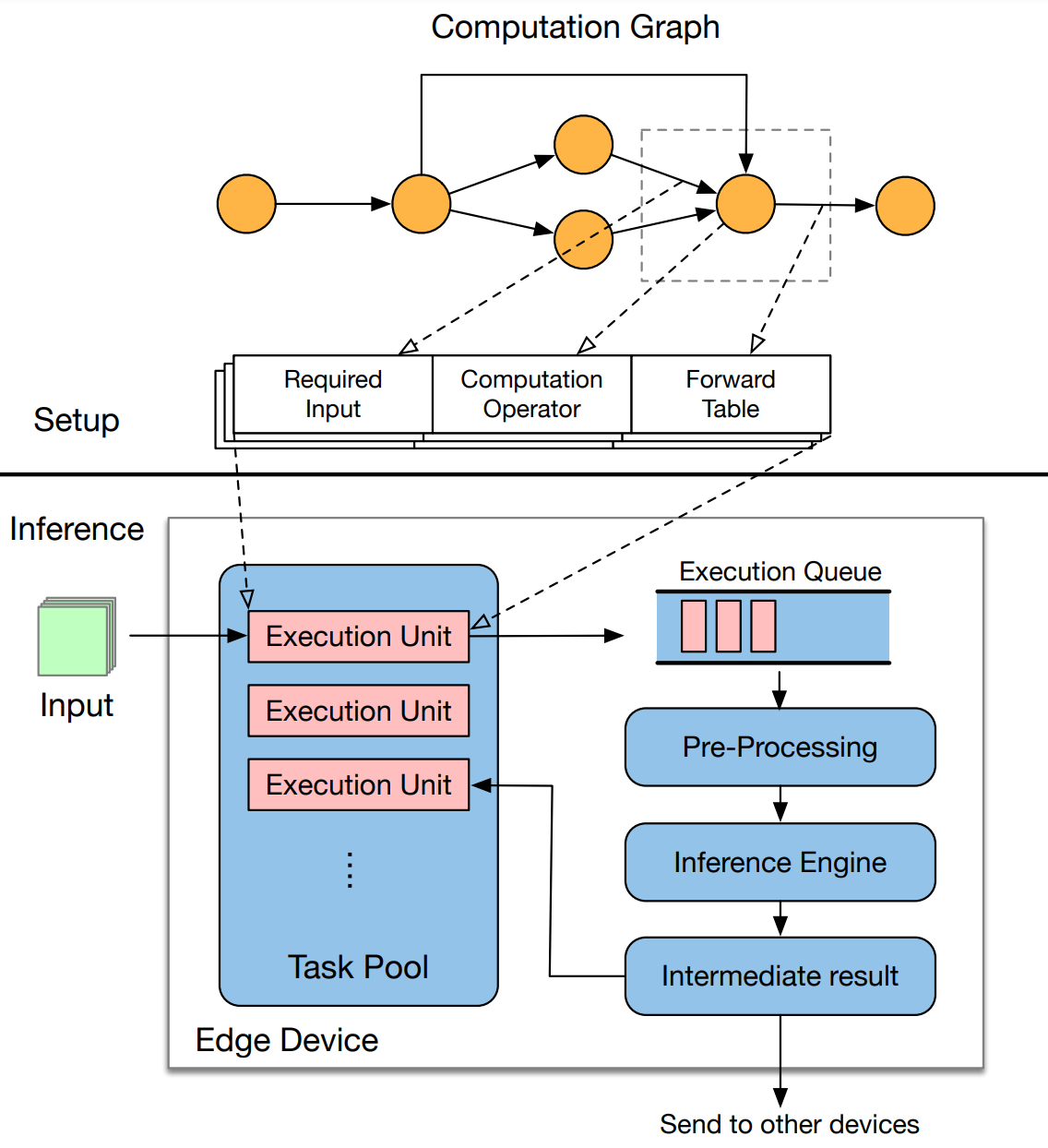
Figure: Our proposed architecture of distributed inference with a DAG structured model: (1) partitioning the model in the Setup Phase; (2) collaborating with other devices to serve requests in the Inference Phase.
The figure above shows the mechanism of our distributed inference paradigm. We also need a policy to find the optimal model partitioning scheme to minimize the inference latency. For any specific layer $l$ that has been assigned to device $i,$ the finish time can be estimated as the sum of the computation time $t_{\mathrm{comp}}(i;l),$ and the communication time $t_{\mathrm{trans}}(i;l).$ The computation time can be roughly considered as a linear function of the assigned workload, and we estimate the communication time by
$$t_{\mathrm{trans}}(i;l) = \mathop{\max}_{j\in \{1,\dots,n\}, m\in M}\mathbf{1}_{\{p_{m,i,j} > 0\}}(T_{m,j} + \frac{p_{m,i,j}}{B_{i,j}})\label{eq:trans_time}$$
which can be interpreted as the transmission time of the required inputs plus the time spent on waiting for these inputs to be generated from previous layers. Combining them together, we can formulate the partition decision of a given layer as the following optimization problem:
$$\begin{align}\mathop{\min}_{x} &\quad \max(T_{l,1}, T_{l,2}, \dots, T_{l,n}) \label{eq:raw_opt} \\ s.t. &\quad x_i \in \mathbf{Z^+}, i=0,1,\dots,n \\ &\quad x_0 = 0, x_n = H \\ &\quad x_0 \leq x_1 \leq \dots \leq x_n \end{align}$$
Unfortunately, the formulation above may not be practical to solve, as solving integer programming problems is NP-hard in general. In this context, another highlight in our contributions is that we are able to transform such an integer programming problem to a linear programming (LP) problem as an approximation, such that it can be solved to optimality efficiently, without resorting to heuristics. Our transformed LP problem can then be solved efficiently using off-the-shelf LP solvers. Authored by Chenghao Hu, this work has been published in the Proceedings of IEEE INFOCOM 2022.