With the growth of machine learning, today, deep neural networks (DNNs) have been widely used in many real-world applications, and the size of DNNs is becoming exceedingly large. To train DNNs with hundreds of millions of parameters, it is common to use a cluster of accelerators, e.g., GPUs and TPUs, to speed up the training process. Thus, there is a need to coordinate the accelerators to train DNNs efficiently, which refers to the device placement problem.

The decision of placing parts of the neural network models on devices is often made by human experts based on simple heuristics and intuitions, which are typically not flexible for a dynamic environment with many interferences. Deep reinforcement learning (DRL) has recently been proposed to provide effective device placements with full automation. However, existing DRL-based solutions experience slow convergence of the learning process, especially for large models such as BERT.

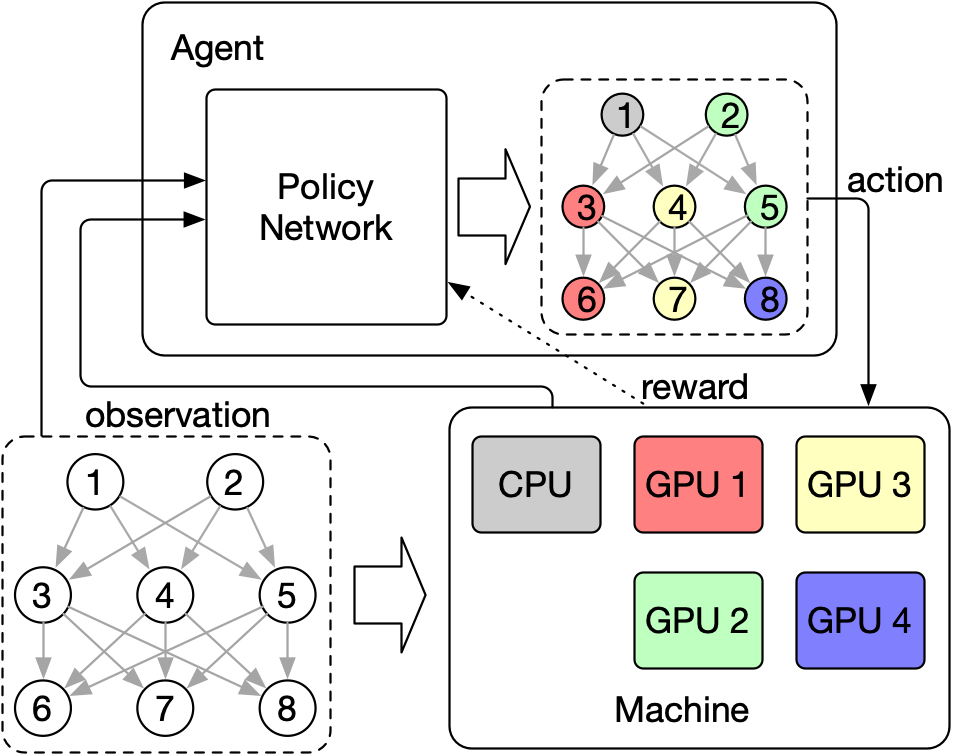
An illustration of DRL-based framework for device placement problem.

In this work, we present Mars, a new DRL-based device placement framework that is fast and can be scalable to very large models. Mars adopts a graph neural network (GNNs) to encode the workload information and capture the topological properties of the computational graph. In additionally, Mars employs self-supervised pre-training of its graph encoder in its design, which achieves a further performance improvement. The encoded representations are then fed into a segment-level sequence-to-sequence neural network to generate placement. The entire DRL agent is trained by an advanced DRL training algorithm, Proximal Policy Optimization (PPO).

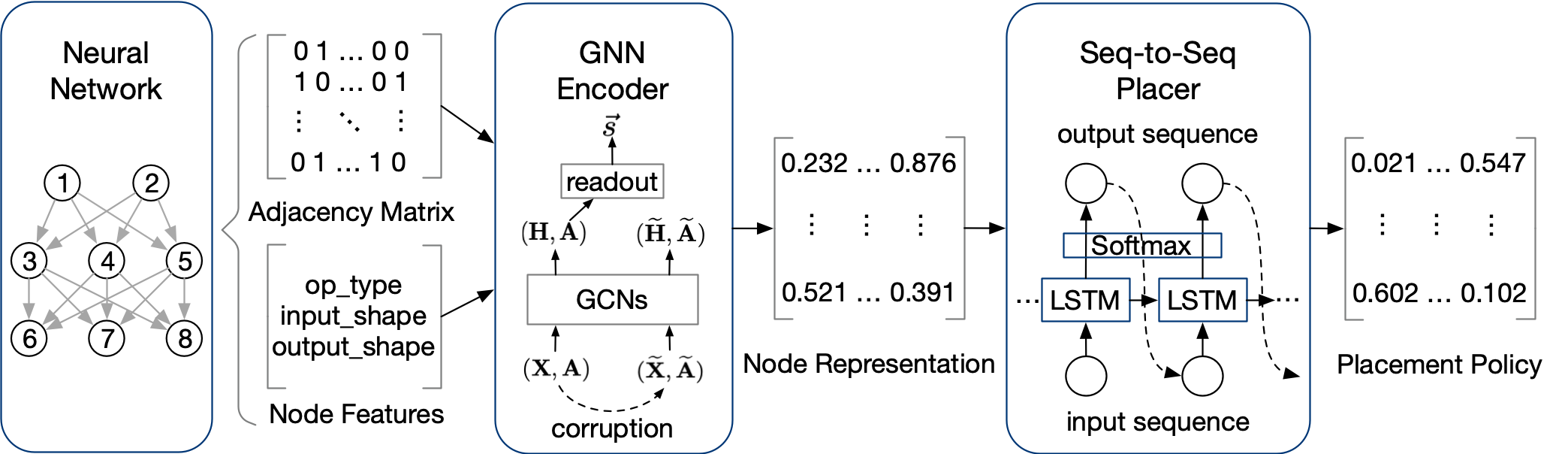
An overview of Mars framework.

The device placement problem is to identify an optimal placement across devices for a machine learning workload, which can be described as a computational graph that consists of thousands of operation nodes with various attributes. For extracting the underlying information from such graph-structured data, Mars employs a GNN as an encoder and pre-trains it in a self-supervised fashion with contrastive learning.

Specifically, we first generate a pair of samples in different augmented views, where the positive samples $(\mathbf{X},\mathbf{A})$ is as the same as the original graph and the negative samples $(\widetilde{\mathbf{X}},\widetilde{\mathbf{A}})$ is the graph augmented by a corruption function $\mathcal{C}(\cdot)$. Then, we generate the node representations $\mathbf{H}$ and $\widetilde{\mathbf{H}}$ (local information) by GNN, and the graph-level representation $\vec{s}$ (global information) of positive samples by a mean-pooling readout function:

$$\mathcal{R}(\mathbf{H}) = \sigma\left(\frac{1}{N} \sum_{i=1}^{N} \vec{h}_{i}\right)$$

Next, we use a simple bilinear scoring function to score the mutual information between local information $\vec{h}_{i}$ and the global summary $\vec{s}$. A logistic sigmoid nonlinearity is applied to convert scores into probabilities:

$$\mathcal{D}\left( \vec{h}_{i}, \vec{s} \right) = \sigma\left( \vec{h}_{i}^{T}\mathbf{W}\vec{s} \right)$$

Finally, we minimize the Jensen-Shannon divergence between the probabilities of $(\vec{h}_{i}, \vec{s})$ being a positive example and $(\vec{\tilde{h}}_{i}, \vec{s})$ being a negative example: $$\mathcal{L} = \frac{1}{N+N} \left( \sum_{i=1}^{N} \mathbb{E}_{(\mathbf{X},\mathbf{A})} \left[ \log \mathcal{D}\left( \vec{h}_{i}, \vec{s} \right) \right] + \sum_{j=1}^{N} \mathbb{E}_{(\widetilde{\mathbf{X}},\widetilde{\mathbf{A}})} \left[\log \mathcal{D}\left( \vec{\tilde{h}}_{j}, \vec{s} \right) \right] \right)$$ Therefore, we can gradually learn informative node representations throughout our self-supervised pre-training methods. The pre-trained graph encoder can be directly used for the next step and also can be fine-tuned during the DRL training.

The encoded node representations of operations are then fed into our sequence-to-sequence placer to generate the placement of DNN workload. However, there are over thousands of operations in the DNN, and the sequence-to-sequence neural network are known not good at handling the long sequence. Thus, Mars adopts the segment-level sequence processing that divides the long operation sequence into smaller segments and places them segment-by-segment.

We evaluate Mars by training it to produce device placement solutions for three benchmark machine learning models, i.e., InceptionV3, GNMT, and BERT. The per-step execution times of our final placements are compared with the state-of-the-art, i.e., Hierarchical Planner and Generalized Device Placement (GDP). Experimental results have demonstrated that the per-step execution time of the best placement discovered by Mars for GNMT and BERT is 2.7% and 27.2% shorter than the placements found by Hierarchical Planner. In addition, Mars achieves better training efficiency than the state-of-the-arts, it reduced its training time by an average of 13.2% via self-supervised pre-training.

Hao Lan is the first author of this work. It has been published in 51st the International Conference on Parallel Processing ICPP 2021.